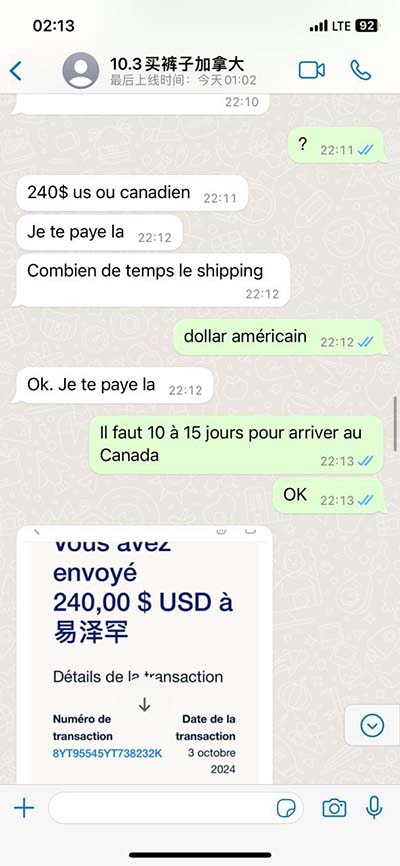
replicating omega frequency | Why are angular frequencies $\\omega=2\\pi f$ used over normal replicating omega frequency • Cycle per second• Radian per second• Degree (angle)• Mean motion• Rotational frequency See more
Louis Vuitton’s range of phone cases, bumpers and folios for women combine function with fashion. These stylish iPhone accessories are offered in a variety of sizes and signature materials, including models that recall the House’s trunk-making legacy.
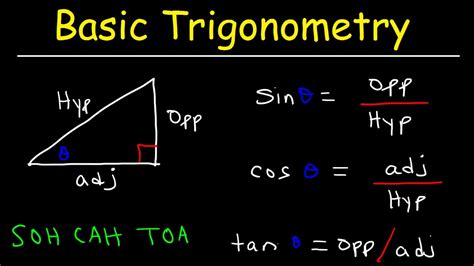
0 · trigonometry
1 · sampling
2 · Why are angular frequencies $\\omega=2\\pi f$ used over normal
3 · What is the significance of angular frequency $\omega$ with
4 · Mechanisms of Theta Plasmid Replication
5 · Is it real? A buyer's guide to spotting a fake Omega
6 · Angular frequency
7 · Amplitude, Frequency, Wave Number, Phase Shift
8 · 9.2: DNA Replication
9 · 6.02 Practice Problems: Modulation & Demodulation
TRANSMAX ATF DEXRON®- VI MERCON® LV Multivehicle is approved and licenced by GM and Ford for use in vehicles requiring their latest ATF specifications and also exceeds the requirements of the JASO-1A for use in most Asian automatic transmissions.Castrol Transmax Dexron® VI Mercon® LV is a premium full synthetic transmission fluid, formulated with Smooth Drive Technology™. It delivers outstanding sludge resistance to provide superior transmission life and enhanced friction to .
In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or . See moreIn SI units, angular frequency is normally presented in the unit radian per second. The unit hertz (Hz) is dimensionally equivalent, but by convention it is only used for frequency f, . See moreAlthough angular frequency is often loosely referred to as frequency, it differs from frequency by a factor of 2π, which potentially leads confusion when the distinction is not made clear. See moreRelated Reading:• Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe. New York City: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8. See more
Circular motionIn a rotating or orbiting object, there is a relation between distance from the axis, $${\displaystyle r}$$, tangential speed, $${\displaystyle v}$$, and the angular frequency of the rotation. During one period, See more• Cycle per second• Radian per second• Degree (angle)• Mean motion• Rotational frequency See more
To get the frequency domain representation of this modulated signal, we replicate the spectrum of the original signal at \(-\Omega_c\) and \(+\Omega_c\), scaling each of these replications by . I wanted to "rediscover" the replication of the signal spectrum by pure algebraic manipulation from ejθ or cos(θ + ϕ). First you have to understand where images come from. . It's just nicer to name \pi f$ term as angular frequency $\omega$,- as it gives dimensions $[\text{rad/s}] \equiv [\text{rad} \cdot \text{Hz}]$. That's why it is sometimes called .The angular frequency is related to a quantity often labeled f f and also called the frequency by \omega = 2\pi f ω = 2πf. With these new definitions, solutions to the wave equations can be .
The frequency of replication initiation is tightly regulated to facilitate establishment in permissive hosts and to achieve a steady state. The last section of the article reviews how . You could consider omega to be a pure indicator of periodicity in the cycle. Larger omega gives you more rads per second. Larger omega gives you shorter wavelength, and . The reason we use the angular frequency, $\omega$, is because the \pi$ is always present and so to know how quickly the function repeats, i.e. to have an intuitive idea . The replication of DNA occurs during the synthesis phase, or S phase, of the cell cycle, before the cell enters mitosis or meiosis. The elucidation of the structure of the double .
It should have a unique identifying serial number engraved on the case, which you can check against Omega's records. Fake Omega watches are among the most common kinds of .
trigonometry
sampling
In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase .To get the frequency domain representation of this modulated signal, we replicate the spectrum of the original signal at \(-\Omega_c\) and \(+\Omega_c\), scaling each of these replications by .
I wanted to "rediscover" the replication of the signal spectrum by pure algebraic manipulation from ejθ or cos(θ + ϕ). First you have to understand where images come from. .
Both processes are given from the shift property of the Fourier Transform which states that multiplying a function $x(t)$ in the time domain by $e^{j\omega_c t}$ will shift the . It's just nicer to name \pi f$ term as angular frequency $\omega$,- as it gives dimensions $[\text{rad/s}] \equiv [\text{rad} \cdot \text{Hz}]$. That's why it is sometimes called .The angular frequency is related to a quantity often labeled f f and also called the frequency by \omega = 2\pi f ω = 2πf. With these new definitions, solutions to the wave equations can be .
The frequency of replication initiation is tightly regulated to facilitate establishment in permissive hosts and to achieve a steady state. The last section of the article reviews how .$\omega$: Normalized radian frequency. $\omega = \Omega/F_s = 2\pi F/F_s$. Sometimes its units are listed as being radians/sample. Because of aliasing, it is only necessary to study the . You could consider omega to be a pure indicator of periodicity in the cycle. Larger omega gives you more rads per second. Larger omega gives you shorter wavelength, and .
The reason we use the angular frequency, $\omega$, is because the \pi$ is always present and so to know how quickly the function repeats, i.e. to have an intuitive idea .In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase .To get the frequency domain representation of this modulated signal, we replicate the spectrum of the original signal at \(-\Omega_c\) and \(+\Omega_c\), scaling each of these replications by .
I wanted to "rediscover" the replication of the signal spectrum by pure algebraic manipulation from ejθ or cos(θ + ϕ). First you have to understand where images come from. . Both processes are given from the shift property of the Fourier Transform which states that multiplying a function $x(t)$ in the time domain by $e^{j\omega_c t}$ will shift the . It's just nicer to name \pi f$ term as angular frequency $\omega$,- as it gives dimensions $[\text{rad/s}] \equiv [\text{rad} \cdot \text{Hz}]$. That's why it is sometimes called .The angular frequency is related to a quantity often labeled f f and also called the frequency by \omega = 2\pi f ω = 2πf. With these new definitions, solutions to the wave equations can be .
The frequency of replication initiation is tightly regulated to facilitate establishment in permissive hosts and to achieve a steady state. The last section of the article reviews how .
$\omega$: Normalized radian frequency. $\omega = \Omega/F_s = 2\pi F/F_s$. Sometimes its units are listed as being radians/sample. Because of aliasing, it is only necessary to study the . You could consider omega to be a pure indicator of periodicity in the cycle. Larger omega gives you more rads per second. Larger omega gives you shorter wavelength, and .

Why are angular frequencies $\omega=2\pi f$ used over normal

davidsw rolex datejust
Assessment of global LV systolic function has an important role in assessing the prognosis of a variety of cardiac diseases, and also influences treatment strategies. 1 The most widely used parameter is LVEF, and this is commonly obtained by echocardiography.
replicating omega frequency|Why are angular frequencies $\\omega=2\\pi f$ used over normal